片元着色器运行次数远多于顶点着色器, 那为什么还说它们是一对一的
需要区分几个概念:
- 顶点(Vertex) 一个几何图形的起始点比如三角形有3个顶点。
- 片元(Fragment / Pixel) 屏幕的一个像素每个片元最终都会呈现一个颜色。
- 顶点着色器(Vertex Shader) 为每个顶点运行处理输入的几何数据计算插值因子等。
- 片元着色器(Fragment Shader) 为每个片元运行处理材质、光照等计算最终颜色。 所以:
- 顶点着色器一次运行对应一个顶点。
- 片元着色器一次运行对应一个片元(屏幕个个像素)。 由于三角形内部的每个片元都是通过插值一个或几个顶点计算出来的。 所以:
- 每个顶点都对应了一个或几个片元。
- 每个片元都对应着一个或几个顶点。 这就产生了一种一对一的映射关系。 因此我们说:
- 顶点着色器和片元着色器是一对一的。
传统着色方法 和 基于物理原理的 PBR 工作流
光照模型 (Lighting Models)
├── 基于经验的光照模型 (Empirical Lighting Models)
│ ├── Lambertian (漫反射)
│ ├── Phong (高光反射)
│ └── Blinn-Phong (改进的高光反射)
└── 基于物理的光照模型 (Physically Based Lighting Models)
│ ├── PBR (基于物理的渲染)
│ │ ├── 金属/粗糙度工作流
│ │ ├── 反射率/粗糙度工作流
│ │ └── 基于微表面的BRDF模型
│ └── BSDF (双向散射分布函数)
│ ├── BRDF (双向反射分布函数)
│ │ ├── Lambertian (漫反射)
│ │ ├── Oren-Nayar (粗糙漫反射)
│ │ ├── GGX (微表面模型)
│ │ └── Cook-Torrance (微表面模型)
│ ├── BTDF (双向透射分布函数)
│ └── Principled BSDF (多功能/迪士尼 BSDF)
Principled BSDF
├── 微表面理论(Microfacet Theory):
│ ├── 表面被建模成由微小的、镜面反射的小平面组成的集合
│ │ ├── 每个小平面都服从菲涅尔方程和 Snell 定律
│ │ └── 微表面的分布函数(例如,GGX 或 Beckmann)决定了表面的粗糙度
│ ├── 菲涅尔方程(Fresnel Equation):
│ │ ├── 描述了光线在不同介质之间传播时反射和折射的比例
│ │ └── 反射率随入射角度变化
│ └── 能量守恒:
│ ├── 确保反射和折射的总能量不超过入射能量
│ └── 避免出现不真实的过亮效果
└── 基于BRDF(双向反射分布函数)和BTDF(双向透射分布函数)的数学模型:
├── BRDF:
│ ├── 漫反射项
│ │ └── 通常使用 Lambertian 模型或改进版本
│ ├── 镜面反射项
│ │ └── 通常使用 GGX, Beckmann等微表面模型
│ └── 基于物理的反射模型 (PBR的核心,包含了菲涅尔效应和微表面模型)
└── BTDF:
├── 透射项
│ └── 使用折射率控制透明度
└── 基于物理的折射模型 (PBR中的透明材质处理)| 时间段/对比项 | 传统着色方法 | 基于物理原理的 PBR 工作流 |
|---|---|---|
| 1970-2000 年代 | 传统着色方法得到广泛使用,使用多边形建模和正算渲染进行实现。这些方法能够产生逼真的效果,但不考虑真实世界中材质和光照的物理属性。 | 计算机图形学的学术研究逐渐探索光线追踪等基于物理原理的渲染方法。 |
| 2003 年 | Pixar 公司发布了基于物理原理的渲染系统,即 RenderMan RIS,这被视为 PBR 工作流的起源。 | 开始出现一些基于物理原理的 PBR 渲染引擎和学术研究,如 Mental Ray、Arnold、OctaneRender、V-Ray、Maxwell Render、Corona Render、Cycles 和 Blender。此时,PBR 工作流被广泛认同并被视为渲染的未来方向。 |
| 2010 年代 | 引擎和软件制造商开始将 PBR 工作流纳入他们的产品中,例如 Unity、Unreal Engine、Blender、Substance Painter 和 Marmoset Toolbag 等。 | PBR 工作流得到越来越广泛地应用,成为游戏和电影制作的行业标准。在游戏中,对于真实感和逼真度的需求促使 PBR 使用越来越广泛,而对于电影的要求则强调对细节和精度的控制。 |
| 光照模型 | 固定的、抽象的光照模型 (如 Phong 或 Blinn-Phong 模型) | 基于物理规律的光照模型 (如 Cook-Torrance 或 GGX 模型),能更准确的模拟真实光照行为。 |
| 着色材质 | 着色材质使用的参数是预定义的,例如反射率和高光度等 | 着色材质使用的参数是基于物理意义的物理属性,例如粗糙度、金属度和折射率等,能更真实地模拟各种材质的效果。 |
| 纹理制作 | 纹理需要手动制作,并且需要大量的手动调整,例如在阴影和高光区域添加或减少纹理 | 纹理的生成依赖于各种物理属性,每个属性都有自己的纹理映射,无需手动调整,并且可以反映出更多的物理效果。 |
| 灯光设置 | 灯光设置需要根据场景进行手动调整,每个场景都需要重新设置灯光 | 灯光设置基于现实光照情况,无需手动调整。PBR 工作流可以更好地应用现实世界中的光照环境,并根据光源的颜色、强度和距离等属性来自动进行计算。 |
| 投影贴图 | 投影贴图的使用在传统着色中不常用 | 基于物理原理的 PBR 工作流可以准确地模拟投影的阴影,在各种材质下都可以获得逼真的效果。 |
| 渲染效果 | 渲染效果通常是基于艺术家的主观意愿进行调整,难以获得真实和逼真的效果 | PBR 工作流能够更准确地模拟真实光照和材质属性,制作出更真实和逼真的效果,能够帮助艺术家更好地实现视觉效果。 |
以下是创建金属/粗糙材质的 PBR 工作流:
- 建立基础色信息。基础颜色将是材质的主要颜色,可以使用 RGB 值或纹理图像来定义它。
- 开始定义粗糙度。粗糙度表示材质表面的粗糙程度。使用白色为光面和黑色为非常粗糙。可以使用灰度级调整该值,而不是黑白两色,以更精细地控制粗糙度。
- 为金属/非金属表面设置反射率。如果材质是金属,反射率将在纹理中表示金属的镜面反射程度。如果材质是非金属,反射率将表示光线反射的强度。可以使用 RGB 值或纹理图像来定义它。
- 添加环境遮蔽。环境遮蔽是表面暴露在环境光下的程度。这可以通过添加值或纹理图像来实现,通常是在不同材质间隙或凸出的边缘位置。
- 添加法线贴图。法线图可以使材质看起来更凸起或凹陷,这可以通过添加 2D 纹理来实现。
- 添加粗糙度贴图。如果您有要模仿的真实材料,则更改粗糙度可能还需要添加粗糙度贴图,以更好地控制该材料的外观。
- 添加自发光。如果您需要使材质发光,则可以添加自发光纹理。这可以使红外材料或灯光看起来更真实。
基础光照模型(Phong模型):
其中包括三个主要成分:1环境光 2漫反射光 3镜面反射光
通过对该变换的转置取逆来得到法向量的正确变换方式。
当vertices变换后,法线向量也相应的需要变换。使用MVMatrix会有一些问题: 在只对一个轴收缩或是剪切变换(shear transformation)时,就如图一样,可能会导致法线失准。那么如何解决呢? 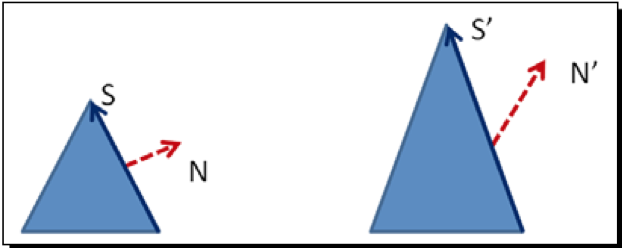 解决方法是使用法线矩阵来变换法线向量。法线矩阵是模型视图矩阵的逆转置矩阵,可以保证在进行任何线性变换时,法线的方向不会发生改变。实现方法如下:
解决方法是使用法线矩阵来变换法线向量。法线矩阵是模型视图矩阵的逆转置矩阵,可以保证在进行任何线性变换时,法线的方向不会发生改变。实现方法如下:
- 首先计算MVMatrix的逆矩阵(保证长度计算正确但不受平移和缩放的影响)
- 对逆矩阵进行转置得到法线矩阵(转置可: 保证方向恢复到原来的方向)
- 将法线向量乘以法线矩阵即可 具体实现代码如下: glm::mat4 MVMatrix = viewMatrix * modelMatrix; glm::mat3 normalMatrix = glm::transpose(glm::inverse(glm::mat3(MVMatrix))); glm::vec3 transformedNormal = normalMatrix * originalNormal; 其中,viewMatrix是视图矩阵,modelMatrix是模型矩阵,originalNormal是原始法线向量,transformedNormal是变换后的法线向量。
为什么矩阵的逆转置,对变换后的点的法线进行变换,就能使得法线朝向正确的方向
- 逆转置矩阵和伴随矩阵有密切关系:
(M⁻¹)ᵀ = adj(M)/det(M), 即一个矩阵的逆转置矩阵可以通过其伴随矩阵和行列式来计算 - 伴随矩阵的几何意义: 伴随矩阵可以被视为是对原矩阵的一种“伴随”变换,这种变换会保留原矩阵变换中的一些性质,比如方向。
- 如果使用变换矩阵
M变换一个切向量t,得到t' = M*t - 如果使用另外一个矩阵
N变换法向量n,得到n' = N*n - 因为法向量和切向量垂直,所以点积
n.t=0 - 变换后,仍然要保证法向量和切向量垂直,所以点积
n'.t'=0 - 即
(N*n) . (M*t) = 0 - 所以
(N*n)ᵀ*(M*t) = 0 - 所以
nᵀNᵀ M t = 0 - 要使得等式成立,那么
NᵀM = I(I是单位矩阵),即Nᵀ = M⁻¹, 所以N = (M⁻¹)ᵀ - 这个推导看起来更像是数学推导,但实际上,它也是在从“维持垂直”这个几何关系进行推导。
摄像头矩阵转换的WebGL的实现
- Theory:
- ObjectCoordinates ModelTransform ViewTransform ProjectionTransform PerspectiveDivision ViewportTransform Viewport(Canvas)Coordinates
- WebGL:
- ObjectCoordinates Model -ViewMatrix PerspectiveMatrix TransformedNormal Vectors gl.viewport Viewport(Canvas)Coordinates
- NormalVectors NommalMatrix 在WebGL中,我们使用3个矩阵以及一个WebGL方法来实现前面说到的5个变换:
- Model-View矩阵包括了model和view变换。
- Normal矩阵通过先对Model-View矩阵求逆再置换的方式获得。
- Perspective矩阵用于projection transformation和perspective division,转化后我们将得到NDC。
- 最后,我们使用
gl.viewport来将NDC映射到视图坐标上,其原型为gl.viewport(minX, minY, width, height)。
摄像头与投影与矩阵
- WebGL中是没有摄像头的,但是我们可以使用MVMatrix创建一个;
- 3D图形经过了很多次变换才被显示在屏幕上,这些变换用一个4*4的矩阵表示;
- 变换都是仿射变换,WebGL通过三个矩阵Modle-View Matrix, Perspective Matrix以及Normal Matrix以及一个WebGL操作gl.viewport()来加以实现;
- 所有的仿射变换都是通过4维数组来变换的,因此我们需要扩充一维w。向量的w值总是0,而点的w值则是1;
- 看WebGL场景时,我们一般都是面向z轴负方向,但是我们也可以通过改变Model-View matrix来改变它;
- Camera Matrix是Model-View matrix的逆矩阵,它们的操作是相反的。我们有两种视角——上帝视角和第一人称视角;
- 当进行仿射变换时,法线需要被特别对待。我们需要从Model-View matrix中计算出新的Normal matrix;
- Perspective决定了两种基本投影方式:即透视投影和正视投影。
省略版的OpenGL渲染流水线(透视投影变换矩阵)

什么是切线空间
- 切线空间(Tangent Space)
- 一种坐标系统
- 用于表达表面几何特征和材质属性
- 计算出这个面片上每个像素的法线向量以及材质纹理的值。
- 使用三组轴:法向量(Normal)、切线向量(Tangent)和副切向量(Bitangent)
- 切线空间描述3D物体表面的几何性质(例如:法线方向),在这个空间中,光照、纹理等都可以进行计算和展示
除了切线空间还有什么空间
- 世界空间描述的是物体在三维空间中的位置和大小,是以场景中心为原点的坐标系。
- 视图空间描述相机观察场景时的状态,是以眼睛所在的位置为原点的坐标系,可以理解为相对于相机的坐标系。
- 投影空间描述的是几何图形如何投射到屏幕上,也称裁剪空间,是一种将三维空间内坐标转化为画面二维坐标的虚拟空间
切线空间与屏幕坐标有什么关系
屏幕坐标指的是渲染后的像素点的位置。渲染过程中,将顶点坐标从世界坐标系转换为摄像机坐标系和投影平面后,最后通过视口变换将投影平面上的坐标换算为屏幕坐标。在这个过程中,也需要使用到切线空间,计算出物体表面的法线贴图、高光贴图等属性,最终使得渲染结果更加真实。
为什么vec4 vertex = uMVMatrix * vec4(aVertexPosition, 1.0); ? vec4(aVertexPosition, 1.0)是什么? 为什么不是vec4(aVertexPosition, 0.0)?
在顶点着色器中,每个顶点的位置需要进行模型视图变换(Model-View Transformation),将模型空间中的顶点坐标变换到观察空间中。这个变换通常包括旋转、平移和缩放,可以用一个4x4的矩阵uMVMatrix表示。因为矩阵乘法是右乘,所以变换的顺序是先缩放、再旋转、最后平移。 vec4(aVertexPosition, 1.0)将顶点坐标从向量形式转换为齐次坐标形式。 如果使用vec4(aVertexPosition, 0.0),那么最终的顶点坐标的w坐标将为0,矩阵乘法中的平移运算将不起作用,顶点将无法正确地变换到观察空间中。
w是什么
在齐次坐标系统中,向量由n+1个元素表示,其中前n个元素为向量的坐标,第n+1个元素为权值。常见的齐次坐标表示方法是使用4个元素表示3维坐标,即(x, y, z, w)。 w的值通常设置为1,这样可以保证在执行模型视图变换和投影变换时,原点(0, 0, 0)的坐标仍然是原点。 如果将w设为0,则表示该向量不是一个点,而是一个方向,用于表示光线的方向、法向量的方向等。 在执行透视除法时,w的值将变为1/w,将坐标从齐次坐标转换为非齐次坐标。
为什么在执行透视除法时,w的值将变为1/w,将坐标从齐次坐标转换为非齐次坐标。举例说明
在透视投影中,离观察者较远的物体在投影平面上呈现的尺寸比较小,而近处的物体则呈现较大的尺寸。为了在投影平面上得到正确的尺寸,需要进行透视除法,将齐次坐标转换为非齐次坐标。 假设有一个点P的齐次坐标表示为(x, y, z, w),那么它的非齐次坐标表示为(x/w, y/w, z/w)。这是因为齐次坐标系中的坐标与非齐次坐标系中的坐标满足以下关系: x/w = x'/w' y/w = y'/w' z/w = z'/w' 其中,x'、y'、z'、w'表示从一个坐标系到另一个坐标系的变换矩阵。 在投影变换中,将物体坐标变换为裁剪坐标,裁剪坐标中的w值通常为-z值。(因为在透视投影中,相机视野内的物体越远,它在投影平面上的大小就越小。为了将远处的物体投影到屏幕上,需要对物体进行缩放,而且缩放的比例应该是和物体距离相反的,即离相机越远,缩放比例越小,远离相机的物体缩放比例应该接近于0。 在投影变换中,使用的是齐次坐标,其中的w值会影响到投影平面上的缩放比例。为了满足上述要求,通常会将物体坐标的z值映射到裁剪坐标系的-w值上。这样,当z越小(离相机越远)时,w值越大(缩放比例越小),投影平面上的物体大小就会和离相机的距离成反比,达到了远近物体的正确缩放比例。同时,这样也方便在投影后进行透视除法,将齐次坐标转换为非齐次坐标。) 然后,通过除以w值,将裁剪坐标转换为标准设备坐标,标准设备坐标的范围为[-1, 1]。这个过程就是透视除法。
例如,裁剪坐标通常表示为C = (x_c, y_c, z_c, w_c),其中w_c是齐次坐标中的齐次分量,表示距离观察者的距离。在裁剪坐标系中,离观察者越远的物体的w_c值越小。
假设有一个物体坐标
P = (x, y, z),并将其变换为裁剪坐标C = (x_c, y_c, z_c, w_c) = (x_p, y_p, -z, z),其中(x_p, y_p, -z, z)是将物体坐标在投影平面上的投影位置。这个变换的目的是将物体坐标从三维空间投影到二维投影平面上,并进行裁剪操作。通过将z坐标变为-z来实现从右手坐标系到左手坐标系的转换。同时,为了在透视除法后得到正确的非齐次坐标(x_p, y_p, z_p),我们需要将w_c的值设为z,这样在透视除法后,就可以通过x_p = x_c / w_c和y_p = y_c / w_c来得到在投影平面上的投影位置。然后,通过除以w值,将裁剪坐标转换为标准化设备坐标NDC(Normalized Device Coordinates)
N = (x_n, y_n, z_n) = (x_c/w_c, y_c/w_c, z_c/w_c)。这样就完成了从物体坐标到标准设备坐标的变换,NDC范围是[-1,1],其中(-1,-1)代表屏幕左下角,(1,1)代表屏幕右上角, 可以将结果传递给图形硬件进行绘制。
平移变换
在三维坐标系中,平移变换可以表示为一个矩阵:
1 0 0 Tx
0 1 0 Ty
0 0 1 Tz
0 0 0 1
顺时针:
1 0 0 0
0 1 0 0
0 0 1 0
Tx Ty Tz 1其中Tx、Ty、Tz是平移的距离,这个矩阵的右下角元素是1,因此与该矩阵相乘的向量不会发生缩放或旋转,只会进行平移。 例如
vec4(2.0, 3.0, 4.0, 1.0) *
mat4(
1.0 0.0 0.0 1.0,
0.0 1.0 0.0 2.0,
0.0 0.0 1.0 3.0,
0.0 0.0 0.0 1.0
) =
vec4(3.0, 5.0, 7.0, 1.0)这个结果就是将顶点坐标(2.0, 3.0, 4.0)进行了平移变换,并转换回了三维坐标。注意到变换矩阵的右下角元素是1.0,这意味着只进行了平移变换,没有进行旋转或缩放。如果右下角元素是0.0,则意味着只进行了旋转或缩放变换。
给出所有变换的矩阵模板
6.5 - Transformation Matrices — LearnWebGL
1. 平移变换矩阵
1 0 0 Tx
0 1 0 Ty
0 0 1 Tz
0 0 0 1其中Tx、Ty、Tz是平移的距离。
2. 旋转变换矩阵逆时针的旋转公式
绕x轴旋转θ角度的变换矩阵:
1 0 0 0
0 cos(θ) -sin(θ) 0
0 sin(θ) cos(θ) 0
0 0 0 1在虚拟3D世界中,正数代表顺时针旋转更容易理解,在实践中更好处理。
顺时针:
1 0 0 0
0 cos(θ) sin(θ) 0
0 -sin(θ) cos(θ) 0
0 0 0 1绕y轴旋转θ角度的变换矩阵:
cos(θ) 0 sin(θ) 0
0 1 0 0
-sin(θ) 0 cos(θ) 0
0 0 0 1
顺时针:
cos(θ) 0 -sin(θ) 0
0 1 0 0
sin(θ) 0 cos(θ) 0
0 0 0 1绕z轴旋转θ角度的变换矩阵:
cos(θ) -sin(θ) 0 0
sin(θ) cos(θ) 0 0
0 0 1 0
0 0 0 1
顺时针:
cos(θ) 0 sin(θ) 0
0 1 0 0
-sin(θ) 0 cos(θ) 0
0 0 0 13. 缩放变换矩阵
Sx 0 0 0
0 Sy 0 0
0 0 Sz 0
0 0 0 1其中Sx、Sy、Sz是分别在x、y、z三个方向上的缩放因子。
4. 拉伸变换矩阵
1 0 0 0
0 1 0 0
0 0 1 0
Tx Ty Tz 1其中Tx、Ty、Tz是在x、y、z三个方向上的拉伸距离。
5. 投影变换矩阵
- 在正交投影中,平行投影线垂直于投影平面。正交投影可以用于创建2D图形和CAD应用程序中的视图。正交投影变换矩阵的模板如下:
2/(r-l) 0 0 -(r+l)/(r-l)
0 2/(t-b) 0 -(t+b)/(t-b)
0 0 -2/(f-n) -(f+n)/(f-n)
0 0 0 1其中,l、r、b、t是投影平面的左、右、下、上边界,n和f是投影平面到视点的距离,表示近平面和远平面的距离。该矩阵是用于执行透视投影变换的。
- 透视投影是一种以类似人类视觉的方式来显示3D场景的技术。在透视投影中,离观察者较远的物体比离观察者较近的物体显得更小。矩阵中的变量l、r、b、t、n和f用于定义投影平面,即将3D场景映射到的平面。左、右、下、上分别表示投影平面的四个边界,而近平面n和远平面f则定义了投影平面到视点的距离。 透视投影矩阵的模板如下:
2n/(r-l) 0 (r+l)/(r-l) 0
0 2n/(t-b) (t+b)/(t-b) 0
0 0 -(f+n)/(f-n) -2fn/(f-n)
0 0 -1 0其中,l、r、b、t、n和f表示投影平面的左、右、下、上、近和远边界。 其中,r-l表示投影平面的宽度,t-b表示投影平面的高度,f-n表示近平面和远平面的距离。 透视投影矩阵的作用是将三维坐标系中的点投影到二维坐标系中,以实现透视效果。在顶点着色器中,通常将模型视图矩阵和投影矩阵相乘,将物体从模型空间转换到裁剪空间。然后,将裁剪坐标除以其w分量,得到标准化设备坐标。最后,将标准化设备坐标变换为屏幕坐标,以在屏幕上显示物体。
dot(N, -L)被用来计算漫反射光的亮度 的意思
dot(N, -L) 表示向量 N 和向量 -L 的点积。点积是两个向量在空间中的投影乘积,其结果是一个标量,可以表示两个向量之间的夹角和长度关系。
- 向量 N 是当前顶点的法向量(垂直于该点表面的向量)
- 向量 -L 是从该点指向光源的向量。
- 因此
dot(N, -L)的值表示光线方向与表面法线方向之间的夹角余弦值,也就是表示光线和表面的相对方向。 - 如果光线方向与表面法线方向越接近,余弦值越大,表面就越接近光线的方向,
webgl的性能瓶颈
- 着色器:着色器编写不当或运行缓慢可能会导致性能下降。
- 图形绘制调用:每个图形绘制调用都会增加CPU中与GPU通信的开销。减少图形绘制调用次数可以优化性能。
- 纹理采样:纹理采样是GPU中的运算密集型操作,可能会影响性能。
- 帧缓冲对象:帧缓冲对象的操作(包括读/写和渲染到帧缓冲对象中)可能导致性能问题。
- 网络传输:在WebGL应用程序中加载大型纹理或模型可能会导致网络传输问题,从而影响性能。
- DOM操作:将WebGL画布插入到DOM中或频繁修改DOM可能会影响性能。
- 设置uniform:设置uniform通常是WebGL中的瓶颈,因为uniform是CPU和GPU之间的数据传输,而CPU和GPU之间的数据传输速度很慢。每次设置uniform都需要将数据从CPU传输到GPU,这会导致额外的延迟和CPU负担,并可能限制WebGL应用程序的性能。
为什么它不用基于上一帧的状态来计算这一帧的状态
一般情况下,基于上一帧状态来计算这一帧状态的方式是非常直观和自然的。但在WebGL中,由于要处理大量的图形数据和复杂的变换操作,这种方式会导致大量的运算和内存占用,从而降低图形的性能和流畅度。 相比之下,基于时间差和初始状态来计算这一帧状态,可以有效地避免导致的性能问题。因为我们只需要保存初始状态和时间差,就可以通过单次运算得到当前帧状态,大大降低了运算量和内存占用。此外,这种方式也可以有效地避免“误差累积”,保证了图形的准确性和稳定性。
w分量可以代表什么
在 WebGL 中,"w" 通常代表齐次坐标(Homogeneous Coordinates)的一部分。在 3D 图形学中,齐次坐标用于表示三维空间中的点或向量,这种表示法的优点是可以通过矩阵乘法来进行各种变换(如平移、缩放、旋转等)。
- 一个齐次坐标通常表示为四维向量 (x, y, z, w)。在大多数情况下,"w" 的值为 1。这样,该坐标就可以被当作是在三维空间中的点。如果 "w" 的值为 0,那么该坐标就表示一个方向,而非一个具体的位置。
- 齐次坐标系统中的缩放因子:在齐次坐标系统中,w可以表示坐标的缩放因子。通过调整w的值,可以对坐标进行缩放操作。
- 透视投影中的深度或距离:在透视投影中,w可以表示从观察者到物体的距离或深度。透视投影会根据距离的远近来调整物体的大小和形状。
- 贝塞尔曲线中的权重:在贝塞尔曲线和曲面的计算中,w可以表示控制点的权重。通过调整w的值,可以影响曲线或曲面上的点的位置和形状。
- 光源中的强度或能量:在计算机图形学中,当表示光源时,w可以表示光的强度或能量。通过调整w的值,可以调整光源对场景的亮度和颜色的影响。
用于投影变换时代表什么
- 在投影变换中,"w" 分量用于保存深度信息
- 这是因为在三维空间中的点投影到二维屏幕上时,我们通常会丢失深度信息(即点离观察者的距离)。通过保留 "w" 分量,我们可以将这个深度信息编码到每个点的齐次坐标中。
- 具体来说,投影矩阵会改变齐次坐标的 "w" 分量,使得它不再始终为 1。
- 然后,为了得到屏幕上的二维坐标,我们需要对齐次坐标进行透视除法
- 即将 "x"、"y" 和 "z" 分量都除以 "w" 分量。这个过程会将坐标的 "w" 分量归一化为 1,同时保留深度信息在 "z" 分量中。
Floating-Point Texture 浮点纹理是什么
- 在计算机图形中,纹理通常被用来存储图像数据,这些数据可以被用来改变3D物体的表面外观。标准的纹理通常包含每一个像素的红色、绿色、蓝色和透明度(RGBA)值,每一个值都是一个8位的整数,范围从0(没有颜色)到255(全颜色)。
- 然而,对于某些高级的图形应用,8位整数的精度可能不够。例如,在物理模拟、光线追踪、高动态范围图像(HDR)等应用中,可能需要更高精度和更大范围的颜色值。这就是浮点数纹理(Floating-Point Texture)的用武之地。
- 浮点数纹理的每个颜色值都是一个浮点数,而不是一个整数。这意味着它们可以有更大的范围(可以是负数,也可以大于1)和更高的精度(可以表示小数)。浮点数纹理通常可以是16位半精度(Half Precision)或32位全精度(Full Precision)。
- 此外,浮点数纹理不仅可以用于存储颜色值,也可以用于存储任何类型的数据。例如,在粒子系统中,可以用浮点数纹理来存储粒子的位置、速度、生命期等属性。
- 然而,使用浮点数纹理也有一些限制和挑战。例如,不是所有的GPU都支持浮点数纹理,或者在某些模式下可能会有性能问题。此外,处理浮点数数据通常要比处理整数数据复杂,特别是在颜色混合和滤波等操作中。因此,使用浮点数纹理需要仔细地考虑其对性能和精度的影响。 对比 WebGL 1 和 WebGL 2,它们的主要区别并不一定直接体现在性能上,而更多体现在功能和效率上。WebGL 2 在 WebGL 1 的基础上增加了许多新的特性和改进,这些特性和改进可以使开发者更高效地利用 GPU 的计算资源,从而间接提高图形和图像处理的性能。
webgl2性能提升
| WebGL 2 的特性 | 对性能的影响 |
|---|---|
| 实例化渲染(Instanced Rendering) | 对性能的提升非常显著,特别是当渲染大量相同的几何体时 |
| 多渲染目标(Multiple Render Targets) | 对性能的提升也很显著,特别是在进行复杂的渲染和后处理操作时 |
| 变换反馈(Transform Feedback) | 对性能的提升较大,特别是在进行复杂的 GPU 计算和物理模拟时 |
| Vertex Array Objects (VAOs) | 在切换不同的几何体和着色器配置时,能显著提升性能 |
| Uniform Buffer Objects (UBOs) | 在处理大量的 Uniforms 时,可以提升性能 |
| 支持更多的纹理格式和数据类型 | 可以提高图形和图像处理的效率,从而间接提升性能 |
| 支持整数和位运算(Integer and Bitwise Operations) | 对性能的提升可能不大,但可以让一些算法在着色器中更高效地实现 |
| 3D纹理和多采样渲染缓冲区(3D Textures and Multisample Renderbuffers) | 主要增强了渲染的可能性和质量,对性能的提升可能不显著 |
模型变换、视图变换、和投影变换
步骤 1: 模型变换(Model Transformation)
假设我们有一个立方体,我们首先需要定义它在模型空间(Model Space)中的顶点坐标。模型空间是物体相对于自身原点的坐标空间。
vec3 cubeVertices[8] = {
vec3(-1.0, -1.0, 1.0), // 顶点 0
vec3(1.0, -1.0, 1.0), // 顶点 1
vec3(1.0, 1.0, 1.0), // 顶点 2
vec3(-1.0, 1.0, 1.0), // 顶点 3
vec3(-1.0, -1.0, -1.0), // 顶点 4
vec3(1.0, -1.0, -1.0), // 顶点 5
vec3(1.0, 1.0, -1.0), // 顶点 6
vec3(-1.0, 1.0, -1.0) // 顶点 7
};步骤 2: 视图变换(View Transformation)
接下来,我们应用视图矩阵将顶点坐标从模型空间转换到视图空间。这个矩阵代表了相机(观察者)的位置和方向。这个变换就像是确定相机如何看待这个立方体。
mat4 viewMatrix = lookAt(cameraPosition, cameraTarget, upDirection);
vec3 viewSpaceVertices[8];
for (int i = 0; i < 8; ++i) {
viewSpaceVertices[i] = (viewMatrix * vec4(cubeVertices[i], 1.0)).xyz;
}给我lookAt的代码
lookAt 函数用于创建视图矩阵,这个矩阵定义了相机(或观察者)在世界空间中的位置、观察的目标点以及上方向。以下是一个简化版的 lookAt 函数的实现,通常用于计算机图形学和OpenGL或WebGL等图形API中。
vec3 normalize(vec3 v) {
float length = sqrt(v.x * v.x + v.y * v.y + v.z * v.z);
// 确保不除以0
if (length > 0.0) {
return v / length;
}
return v;
}
vec3 cross(vec3 a, vec3 b) {
return vec3(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
mat4 lookAt(vec3 eye, vec3 center, vec3 up) {
vec3 zaxis = normalize(eye - center); // 前向量
vec3 xaxis = normalize(cross(up, zaxis)); // 右向量
vec3 yaxis = cross(zaxis, xaxis); // 上向量
mat4 viewMatrix = mat4(
vec4(xaxis.x, yaxis.x, zaxis.x, 0),
vec4(xaxis.y, yaxis.y, zaxis.y, 0),
vec4(xaxis.z, yaxis.z, zaxis.z, 0),
vec4(-dot(xaxis, eye), -dot(yaxis, eye), -dot(zaxis, eye), 1)
);
return viewMatrix;
}这个函数接受三个参数:
eye: 相机(或观察者)在世界空间中的位置。center: 相机正在观察的点。up: 世界空间中的上方向向量。 函数首先计算出相机的前(z轴)、右(x轴)和上(y轴)向量,然后使用这些向量来构造一个视图矩阵。这个矩阵将用于将坐标从世界空间变换到视图空间。
步骤 3: 投影变换(Projection Transformation)
最后,我们使用投影矩阵将视图空间中的顶点坐标转换到裁剪空间。投影矩阵定义了3D场景如何映射到2D屏幕上,包括视角和裁剪面。
mat4 projectionMatrix = perspective(fov, aspectRatio, nearPlane, farPlane);
vec4 clipSpaceVertices[8];
for (int i = 0; i < 8; ++i) {
clipSpaceVertices[i] = projectionMatrix * vec4(viewSpaceVertices[i], 1.0);
}给我perspective的代码
perspective 函数用于创建透视投影矩阵,这个矩阵定义了一个可视的视锥体,用于确定哪些对象应该被渲染以及它们是如何被映射到屏幕上的。以下是一个基本的 perspective 函数实现,它用于计算机图形学和OpenGL或WebGL等图形API中。
mat4 perspective(float fov, float aspect, float near, float far) {
float tanHalfFovy = tan(fov / 2.0);
mat4 result = mat4(0.0); // 初始化一个0矩阵
result[0][0] = 1.0 / (aspect * tanHalfFovy);
result[1][1] = 1.0 / tanHalfFovy;
result[2][2] = -(far + near) / (far - near);
result[2][3] = -1.0;
result[3][2] = -(2.0 * far * near) / (far - near);
return result;
}
//假设(90度视场,16:9的纵横比,近裁剪面为0.1,远裁剪面为100.0),透视投影矩阵 `result` 如下所示:
[[ 0.5625 0. 0. 0. ]
[ 0. 1. 0. 0. ]
[ 0. 0. -1.002002 -1. ]
[ 0. 0. -0.2002002 0. ]]
//这个矩阵代表了透视投影的变换。它的作用是将视锥体内的点映射到一个标准化的立方体(范围在 [-1, 1] 内的每个维度)中。
//请注意,这个矩阵中的第四列和第四行与普通的仿射变换矩阵不同,这是因为透视投影涉及到齐次坐标和透视除法。 这个函数接受四个参数:
fov: 视场(Field of View),即视锥体的垂直张角,通常以弧度为单位。aspect: 纵横比(Aspect Ratio),通常是画面的宽度除以高度。near: 近裁剪面的距离。far: 远裁剪面的距离。 函数的主要目的是计算一个矩阵,该矩阵将视锥体内的所有坐标映射到一个标准化的立方体内,这个立方体的每个维度的范围都是 [-1, 1]。这个过程包括了透视除法,确保了物体随距离的增加而看起来更小的效果。
渲染管线中的位置
- 在模型空间中,立方体的顶点定义了它的形状和大小。
- 经过视图变换后,在视图空间中,立方体的顶点位置表示了立方体相对于相机的位置和方向。
- 最后,投影变换将这些顶点映射到裁剪空间,准备进行裁剪和最终的屏幕映射。 这个过程中的每一步都是通过矩阵乘法来完成的,这是3D图形渲染中的标准做法。在实际的应用程序中,这些计算通常在顶点着色器中完成。
gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0);是怎么来的,为什么要三个相乘, uPMatrix,uMVMatrix 是怎么来的
- gl_Position的计算公式如下:gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0); 其中,uPMatrix和uMVMatrix分别是投影矩阵和模型视图矩阵,它们是顶点着色器中的uniform变量,通过将这些变换矩阵与顶点位置向量相乘,可以将顶点从模型坐标系(或世界坐标系)转换到裁剪坐标系(或屏幕坐标系)。
- 具体来说,
- uPMatrix是一个4x4的矩阵,用于将裁剪坐标系的坐标转换为标准化设备坐标系的坐标,其中,标准化设备坐标系是一个以屏幕中心为原点,范围在[-1, 1]之间的二维坐标系。
- uMVMatrix是一个4x4的矩阵,用于将顶点从模型坐标系(或世界坐标系)转换到观察坐标系(或相机坐标系),也就是将顶点的位置和朝向从模型空间转换到相机空间。 因此,通过将这两个矩阵相乘,可以将顶点从模型坐标系(或世界坐标系)转换到观察坐标系,然后再将其乘以顶点的位置向量,得到在观察坐标系中的位置。最后,再将其乘以投影矩阵,得到在裁剪坐标系中的位置,最终将这个位置向量写入gl_Position中。 综上所述,gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0)的含义是将顶点从模型坐标系(或世界坐标系)转换到裁剪坐标系(或屏幕坐标系)。
